0. 시작하면서
현업에서 GPU 관련 업무를 수행하고 있지만, 정작 그 내부 구조에 대해서는 깊이 있게 알지 못한다는 아쉬움이 늘 있었습니다. AI라는 영역 역시 업무와 가깝게 맞닿아 있으면서도, 기반 지식이 부족하다 보니 여전히 멀게만 느껴졌습니다. 이에 GPU의 내부 구조와 동작 원리를 밑바닥부터 파악해보고자 센터장님께서 추천해주신 아티클을 공부해보게 되었습니다.
1. 개요
딥러닝 모델을 돌리다 보면 문득 궁금해집니다. "왜 이 알고리즘은 50초가 아니라 50ms가 걸릴까? 혹은 왜 5ms로 줄일 수는 없을까?"
모델 내부에서 실제로 어떤 일이 벌어지고 있길래 시간이 소요되는 걸까요? 오늘은 딥러닝 성능 최적화의 핵심인 연산(Computation)과 통신(Communication), 그리고 이를 분석하는 루프라인(Roofline) 모델에 대해 알아보겠습니다.
2. 시간의 두 가지 축: 연산과 통신
딥러닝 모델의 실행 시간은 크게 두 가지 요소에 의해 결정됩니다.
1. 연산 (Computation)
딥러닝 모델은 본질적으로 수많은 행렬 곱셈의 집합입니다. 이는 부동소수점 곱셈과 덧셈 연산(FLOPs)으로 이루어집니다.
- 속도 결정 요인: 가속기(GPU/TPU)의 연산 속도 (FLOPs/s)
- 예시: NVIDIA H100은 초당 약 9.89e14회의 연산을, TPU v6e는 9.1e14회의 연산을 수행합니다.
2. 통신 (Communication)
연산을 하려면 데이터가 필요합니다. 데이터를 이동시키는 과정이 바로 통신입니다.
- 칩 내부 통신: 메모리(HBM)에서 연산 코어로 텐서를 이동시키는 것 (대역폭: H100 약 3.35TB/s).
- 칩 간 통신: 여러 가속기에 모델을 분산시킬 때 칩끼리 데이터를 주고받는 것.
3. 결론적으로 총 소요 시간은?
보통 연산과 통신은 동시에 진행될 수 있습니다. 따라서 전체 시간은 둘 중 더 오래 걸리는 시간(Maximum)에 의해 결정됩니다.
실행 시간 ≈ max(연산 시간, 통신 시간)
3. 효율성의 척도: 산술 강도 (Arithmetic Intensity)
우리가 하드웨어를 얼마나 알뜰하게 쓰고 있는지 어떻게 알 수 있을까요? 여기서 산술 강도라는 개념이 등장합니다.
- 정의: 데이터 1바이트를 통신(이동)할 때, 몇 번의 연산(FLOPs)을 수행하는가?
- 공식: 총 연산량(FLOPs) / 총 통신량(Bytes)
이 비율이 높다는 것은 데이터를 한 번 가져와서 아주 많이 계산한다는 뜻이므로 효율적입니다. 반대로 비율이 낮으면 데이터만 나르다가 시간이 다 간다는 뜻입니다.
하드웨어의 '임계값' (Peak Arithmetic Intensity)
모든 하드웨어는 자신만의 최적 산술 강도 임계값을 가집니다.
- 예를 들어, TPU v5e의 임계값은 약 240 FLOPs/Byte입니다.
- 내 알고리즘의 산술 강도가 240보다 낮다? → 통신 집약적 (Communication-bound): 메모리 대역폭 때문에 성능 저하.
- 내 알고리즘의 산술 강도가 240보다 높다? → 연산 집약적 (Compute-bound): 하드웨어의 연산 능력을 100% 활용 중.
4. 루프라인(Roofline) 모델
이 관계를 그래프로 그린 것이 바로 루프라인 플롯입니다.
- X축: 산술 강도 (Arithmetic Intensity)
- Y축: 처리량 (FLOPs/s)
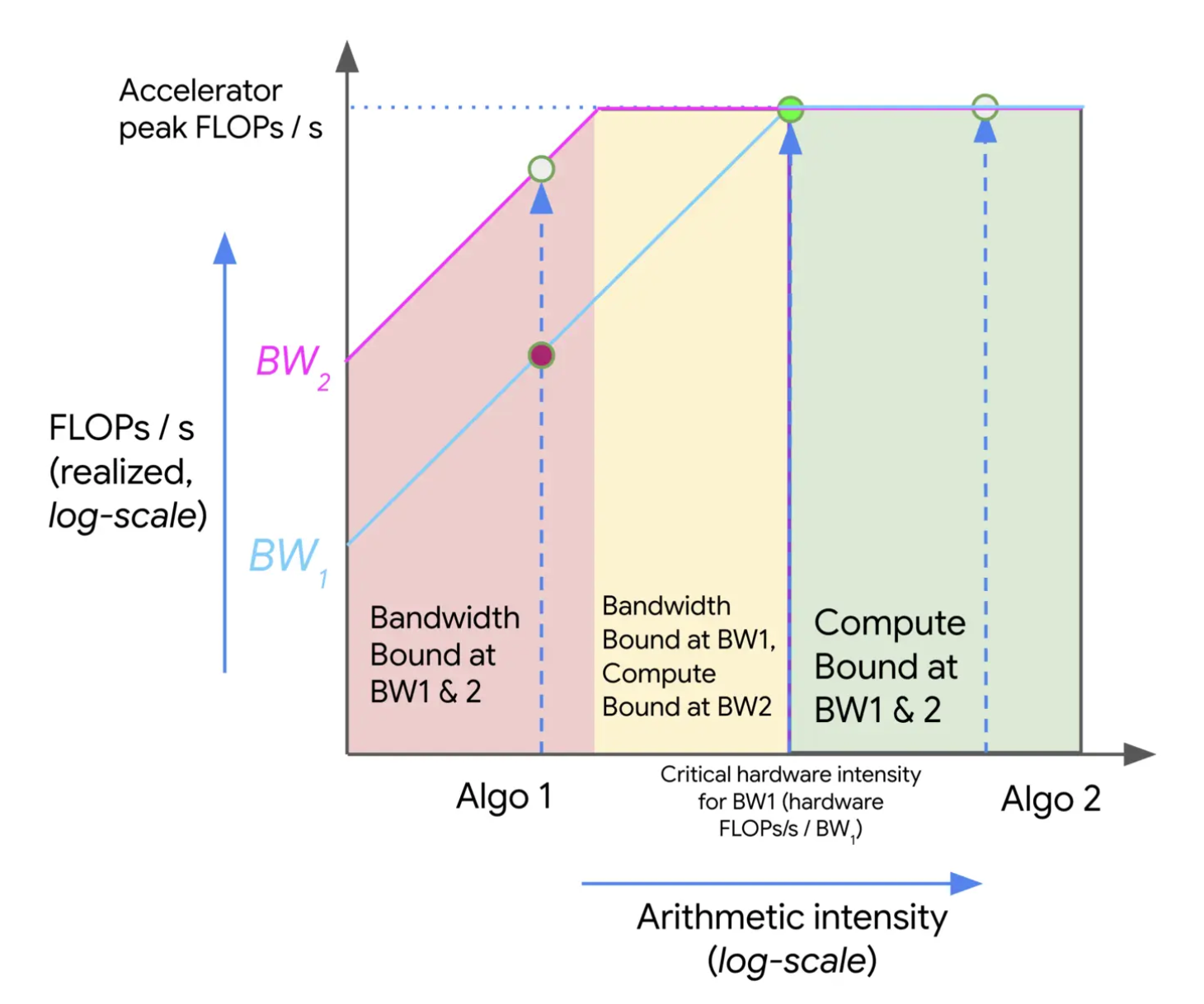
그래프는 지붕 모양을 하고 있습니다.
- 경사면 (왼쪽): 산술 강도가 낮은 영역. 여기서는 아무리 연산 장치가 좋아도 메모리 대역폭(Bandwidth)에 막혀 성능이 오르지 않습니다. (빨간색 영역)
- 지붕의 평평한 면 (오른쪽): 산술 강도가 임계값을 넘은 영역. 이제 메모리 속도는 문제가 안 되며, 하드웨어의 최대 연산 속도를 온전히 누릴 수 있습니다. (초록색 영역)
5. 실전 적용: 행렬 곱셈(MatMul)과 배치 크기
"그래서 어떻게 최적화하나요?"
트랜스포머 모델의 핵심인 행렬 곱셈을 예로 들어봅시다.
단순한 벡터 내적은 산술 강도가 0.5에 불과해 항상 메모리 속도에 발목을 잡힙니다. 하지만 거대 행렬 곱셈은 다릅니다.
"왜 거대 행렬 곱셈은 다를까요? 비밀은 '재사용'에 있습니다."
1. 단순 벡터 내적 (Dot Product)
길이가 N인 두 벡터 x와 y를 곱해서 스칼라 값 하나를 만드는 연산입니다.
- 가정: N = 4,096
- 연산: x⋅y = ∑(xi×yi)
① 메모리 전송량 (Bytes)
- 벡터 x 로딩: 4,096 × 2 Bytes = 8,192 Bytes
- 벡터 y 로딩: 4,096 × 2 Bytes = 8,192 Bytes
- 결과값 저장: 2 Bytes
- 총 전송량 ≈ 16,384 Bytes
② 연산량 (FLOPs)
- 곱셈 N번 + 덧셈 번 = 2N
- 2 × 4,096 = 8,192 FLOPs
- 총 연산량 = 8,192 FLOPs
③ 산술 강도 (효율)
8,192 FLOPs / 16,384 Bytes = 0.5
결론: 데이터 2바이트 가져와서 연산 1번 합니다. 데이터 재사용이 전혀 없습니다.
2. 거대 행렬 곱셈 (Matrix Multiplication)
크기가 N×N 인 두 행렬 A와 B를 곱해서 행렬 C를 만드는 연산입니다.
- 가정: N = 4,096 (위와 동일한 차원 크기)
- 연산: C = A × B
① 메모리 전송량 (Bytes)
- 행렬 A 로딩: 4,096 × 4,096 × 2 = 33,554,432 Bytes
- 행렬 B 로딩: 4,096 × 4,096 × 2 = 33,554,432 Bytes
- 행렬 저장: 4,096 × 4,096 × 2 = 33,554,432 Bytes
- 총 전송량 ≈ 100,663,296 Bytes (약 100 MB)
② 연산량 (FLOPs)
- 행렬 곱셈의 연산량 공식: 2 × N^3
- 2 × 4,096^3 ≈ 137,438,953,472 FLOPs
- 총 연산량 ≈ 1,374 억 FLOPs
③ 산술 강도 (효율)
137,438,953,472 FLOPs / 100,663,296 Bytes ≈ 1,365.3
결론: 데이터 1바이트 가져와서 1,365번이나 연산합니다.
행렬 A의 한 줄(Row)과 행렬 의 한 열(Column)을 가져오면, 그 안의 숫자들은 곱셈 과정에서 N번씩 계속 재사용되기 때문입니다.
3. 최종 비교 요약
| 벡터 내적 | 거대 행렬 곱셈 | |
| 데이터 재사용 | 없음 (1회 사용 후 버림) | 엄청남 (N번 재사용) |
| 산술 강도 | 0.5 | 약 1,365 |
| 하드웨어 상태 | 메모리 병목 (Memory-bound) 데이터 기다리느라 칩이 놂 |
연산 병목 (Compute-bound) 칩이 100% 풀가동함 |
간단히 정리하면, 배치 크기(Batch Size)가 산술 강도를 결정하는 핵심 변수가 됩니다.
💡 핵심 룰 (Rule of Thumb)
bfloat16 행렬 곱셈이 하드웨어 성능을 100% 끌어내기 위한 조건:
- TPU: 칩당 배치 크기 > 240 토큰 (TPU의 임계값이 240 FLOPs/Byte 이기 때문)
- GPU: 칩당 배치 크기 > 약 300 토큰 (GPU의 임계값이 330 FLOPs/Byte 이기 때문)
즉, 배치 크기를 충분히 키워야만 비싼 GPU/TPU가 데이터를 기다리며 노는 시간을 없앨 수 있습니다.
6. 확장: 네트워크 통신 병목
칩 하나를 쓸 때는 메모리 대역폭이 문제였지만, 여러 칩을 연결해 쓸 때는 칩 간 네트워크 대역폭이 새로운 병목이 됩니다.
예를 들어 두 개의 TPU에 행렬을 쪼개서 계산할 때, 연산 시간은 절반으로 줄어들지만 데이터를 주고받는 통신 시간이 추가됩니다. 이때는 배치 크기뿐만 아니라 행렬의 차원 크기가 병목 여부를 결정하는 중요한 기준이 됩니다.
요약
- 딥러닝 속도는 연산 시간과 통신 시간 중 더 느린 쪽에 의해 결정됩니다.
- 산술 강도(FLOPs/Byte)가 하드웨어의 임계값보다 높아야 최고의 성능을 낼 수 있습니다.
- 일반적으로 배치 크기를 키우면 산술 강도가 높아져 '연산 집약적(Compute-bound)' 상태가 됩니다. (TPU 기준 배치 240 이상 권장)
이 글은 딥러닝 하드웨어 성능 분석에 관한 기술 문서를 바탕으로 재구성되었습니다.
'AI > GPU' 카테고리의 다른 글
| 2. TPU란 무엇인가? (0) | 2026.01.25 |
|---|

댓글