백준 25682 : 체스판 다시 칠하기 2
난이도 : 골드 5
시간 : 58분
문제
https://www.acmicpc.net/problem/25682
25682번: 체스판 다시 칠하기 2
첫째 줄에 정수 N, M, K가 주어진다. 둘째 줄부터 N개의 줄에는 보드의 각 행의 상태가 주어진다. B는 검은색이며, W는 흰색이다.
www.acmicpc.net

풀이 과정
체스판은 심플하게 2가지 버전이 있다.
가장 왼쪽, 위쪽의 타일이 흰색인 버전과 검은색인 버전이 있다.
쉽게 W와 B라고 칭하겠다.
이 문제는 누적합과 dp를 사용하면 풀 수 있는 문제이다. 아래 문제를 풀지 않았다면 먼저 풀고 오는 것을 추천한다.
2023.03.02 - [study/Algorithms] - [C++] 백준 11660 - 구간 합 구하기 5
[C++] 백준 11660 - 구간 합 구하기 5
백준 11660 : 구간 합 구하기 5 난이도 : 실버 1 시간 : 자력 x 문제 https://www.acmicpc.net/problem/11660 11660번: 구간 합 구하기 5 첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024,
gamxong.tistory.com
Wdp[i][j] : (1,1) 부터 (i, j) 까지 W버전일 때 다시 칠해야 하는 횟수
Bdp[i][j] : (1,1) 부터 (i, j) 까지 B버전일 때 다시 칠해야 하는 횟수
부분 코드 설명
string b[2] = {"BW", "WB"};
string w[2] = {"WB", "BW"};
if(board[i][j] != b[(i-1)%2][(j-1)%2]){
Bdp[i][j] = Bdp[i-1][j] + Bdp[i][j-1] - Bdp[i-1][j-1] + 1;
}else{
Bdp[i][j] = Bdp[i-1][j] + Bdp[i][j-1] - Bdp[i-1][j-1];
}위의 코드는 최종코드의 일부이다. 먼저 현재 가지고 있는 보드의 특정 위치가 W 또는 B 버전일 때 칠해야 하는 색과 일치하는지 확인한다.
위의 코드는 B 버전일 때 검사하는 것으로 W버전도 변수 이름만 다를 뿐 동일하다.
먼저 나는 board의 인덱스가 1부터 시작하는 것을 선호하기 때문에 b 배열의 인덱스가 살짝 복잡하게 되어 있다.
하지만 결국 의미는 B부터 시작해서 1,3,5와 같은 홀수 행은 BWBWBW~~ 순서와 2,4,6과 같은 짝수 행은 WBWBWB~~ 순서와 같은지를 확인하는 것이다.
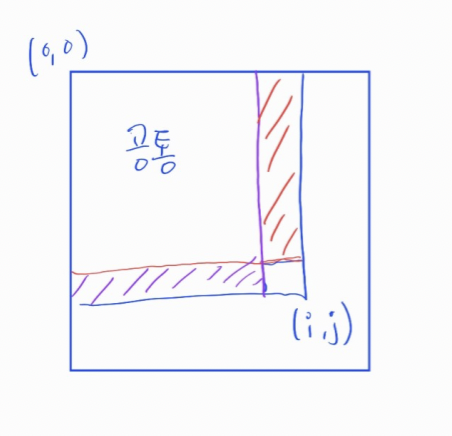
Bdp[i][j] 는 (1,1)부터 (i,j)까지의 다시 칠해야 하는 횟수를 나타낸다고 했다.
따라서 Bdp[i][j]를 구하기 위해서는 이전에 구한 합에서 다시 칠해야 하면 +1를 하고 그렇지 않으면 +0를 하면 된다.
dp[i-1][j-1](공통 영역)를 빼주는 이유는 dp[i][j-1](보라색 영역) + dp[i-1][j](빨간색 영역) 연산을 하면 dp[i-1][j-1]이 2번 더해지기 때문이다.
특정 구간의 합을 구할 때는 아래와 같은 식으로 풀면 된다.
tb = Bdp[K+i][K+j] - Bdp[i][K+j] - Bdp[K+i][j] + Bdp[i][j];
tw = Wdp[K+i][K+j] - Wdp[i][K+j] - Wdp[K+i][j] + Wdp[i][j];(K+i, K+j)까지의 구간을 구한 뒤 (i+1, j+1) 구간부터 (K+i, K+j) 구간을 제외한 구간을 빼준다.
마지막에 Bdp[i][j]를 해준 이유는 해당 구간이 2번 뺄셈되기 때문이다.
최종 코드
#include <iostream>
#include <cstring>
#include <algorithm>
#include <climits>
using namespace::std;
#define MAX 2001
string b[2] = {"BW", "WB"};
string w[2] = {"WB", "BW"};
int board[MAX][MAX];
int Bdp[MAX][MAX];
int Wdp[MAX][MAX];
int N, M, K;
int main(){
scanf("%d %d %d", &N, &M, &K);
for(int i=1; i<=N; i++){
string tmp;
cin >> tmp;
for(int j=1; j<=M; j++){
board[i][j] = tmp[j-1];
}
}
for(int i=1; i<=N; i++){
for(int j=1; j<=M; j++){
if(board[i][j] != b[(i-1)%2][(j-1)%2]){
Bdp[i][j] = Bdp[i-1][j] + Bdp[i][j-1] - Bdp[i-1][j-1] + 1;
}else{
Bdp[i][j] = Bdp[i-1][j] + Bdp[i][j-1] - Bdp[i-1][j-1];
}
if(board[i][j] != w[(i-1)%2][(j-1)%2]){
Wdp[i][j] = Wdp[i-1][j] + Wdp[i][j-1] - Wdp[i-1][j-1] + 1;
}else{
Wdp[i][j] = Wdp[i-1][j] + Wdp[i][j-1] - Wdp[i-1][j-1];
}
}
}
int tb = 0;
int tw = 0;
int min = INT_MAX;
for(int i=0; i<=N-K; i++){
for(int j=0; j<=M-K; j++){
tb = Bdp[K+i][K+j] - Bdp[i][K+j] - Bdp[K+i][j] + Bdp[i][j];
tw = Wdp[K+i][K+j] - Wdp[i][K+j] - Wdp[K+i][j] + Wdp[i][j];
int tmp;
tb < tw ? tmp = tb : tmp = tw;
tmp < min ? min = tmp : 1;
}
}
printf("%d\n", min);
}
잡담
어제 비슷한 문제를 풀어서 그런지 구현하는데는 시간은 좀 걸렸어도 큰 어려움은 없었다.
'PS' 카테고리의 다른 글
| [C++] 백준 2638 - 치즈 (직관적인 접근) (1) | 2023.03.03 |
|---|---|
| [C++] 백준 1918 - 후위 표기식, 반례 (0) | 2023.03.03 |
| [C++] 백준 11660 - 구간 합 구하기 5 (0) | 2023.03.02 |
| [C++] 백준 1920 - 수 찾기 (0) | 2023.03.02 |
| [C++] 백준 12865 - 평범한 배낭 (0) | 2023.03.02 |




댓글