백준 12865 : 평범한 배낭
난이도 : 골드 5
시간 : 해결 x
문제
https://www.acmicpc.net/problem/12865
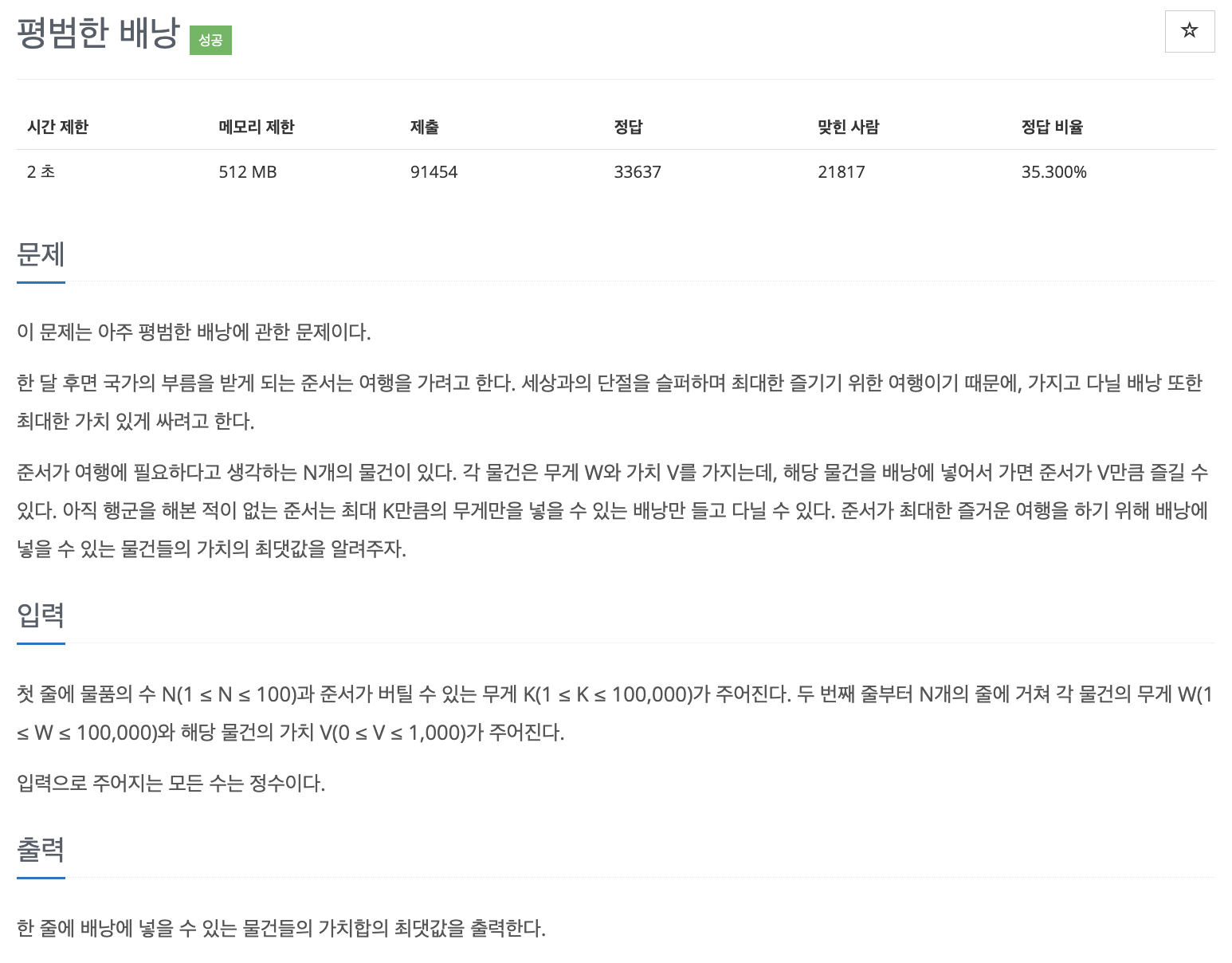
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
풀이 과정
자력으로 풀어보려고 했지만 도저히 해결 방법이 나오질 않아 정답을 참고했다.
먼저 다음과 같은 dp[i][j] 배열을 정의한다.
dp[i][j] = 처음부터 i번째까지의 물건을 살펴보고, 배낭의 용량이 j였을 때 배낭에 들어간 물건의 가치합의 최댓값
먼저 이 dp라는 2차원 배열을 명확히 아는 것이 중요하다.
dp[i][j] = dp[i-1][j];또한, dp[i-1][j]는 가장 최근에 업데이트 시킨 해당 용량일 때의 가치합의 최댓값이다.
따라서 이 코드를 쓰는 것은 맥락이 이해가 갔다.
dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]]+v[i]);하지만 해당 코드에서 dp[i-1][j-w[i]]+v[i] 으로 왜 이렇게 복잡하게 되어있는지 맥락이 이해가질 않았다.
조금 고민해보니 해답을 얻을 수 있었다.
먼저 max의 첫 번째 인자는 해당 위치에 새로운 물건(i번째 물건)를 넣지 않는 경우이다.
새로운 물건을 넣지 않기 때문에 가장 최댓값이었던 dp[i-1][j] 를 그대로 넣어주는 것이다.
max의 두 번째 인자는 해당 위치에 새로운 물건(i번째 물건)를 넣는 경우이다.
새 물건을 넣기 때문에 dp[i-1][j-w[i]] 의 의미는 새 물건의 무게만큼 뺀 용량에서의 최댓값이다.
그 후, 새 물건의 용량만큼 가방을 비워뒀기 때문에 +v[i] 를 할 수 있는 것이다.
해당 문제의 예제1로 예를 들어보자
i = 3, j = 3 일때 --> w[3] = 6이고, max의 두 번째 인자는 dp[2][3-3] 이다.
dp[2][0]은 즉, 2번째까지 물건을 살펴봤을 때 용량 0 일때의 최댓값이다.
용량 0 일때의 최댓값은 아무것도 담을 수 없기 때문에 0이다.
거기에 3번째 물건의 용량을 비워뒀기 때문에 +v[3]를 해서 0+6 = 6의 값이 되는 것이다.
따라서 앞 과정을 반복하여 dp[N][K] 를 출력하면 정답을 출력할 수 있다.
최종 코드
#include <iostream>
#include <algorithm>
#include <string>
using namespace::std;
#define MAX 101
int N, K;
int dp[MAX][100001];
int w[MAX];
int v[MAX];
int main(){
scanf("%d %d", &N, &K);
for(int i=1; i<=N; i++){
scanf("%d %d", &w[i], &v[i]);
}
for(int i=1; i<=N; i++){
for(int j=1; j<=K; j++){
if(j>=w[i]){
dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]]+v[i]);
}else{
dp[i][j] = dp[i-1][j];
}
}
}
printf("%d\n", dp[N][K]);
}
잡담
dp는 항상 어려워..
'PS' 카테고리의 다른 글
| [C++] 백준 11660 - 구간 합 구하기 5 (0) | 2023.03.02 |
|---|---|
| [C++] 백준 1920 - 수 찾기 (0) | 2023.03.02 |
| [C++] 백준 9251 - LCS (0) | 2023.03.02 |
| [C++] 백준 1753 - 최단경로 (0) | 2023.03.02 |
| [C++] 백준 10026 - 적록색약 (0) | 2023.03.01 |




댓글