백준 11444 : 피보나치 수 6
난이도 : 골드 2
시간 : 알고리즘 수업자료 참고
문제
https://www.acmicpc.net/problem/11444
11444번: 피보나치 수 6
첫째 줄에 n이 주어진다. n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다.
www.acmicpc.net

풀이 과정
이 문제를 본 순간 어제 알고리즘 수업에서 배운 피보나치 행렬 풀이법이 기억났다.
따라서 나의 직관으로 풀진 못했고, 배운 내용 + 다른 사람의 코드를 참고하면서 풀었다.

먼저 피보나치 수열의 점화식 F(n+2) = F(n+1) + F(n)을 통해 위 그림과 같은 행렬을 유도할 수 있다.
해당 식을 생각하면 그 이후에는 어렵지 않게 유도할 수 있다.
하지만 어떻게 해당 식을 유도할 수 있을까?
아무 정보도 없이 해당 식을 유도해내는 것은 거의 불가능하다고 생각한다.
Fibonacci matrix

위의 사진이 'Fibonacci matrix'라고 불린다. Fibonacci matrix는 피보나치 수열과 관련하여 처음으로 소개된 것은 19세기 말 프랑스 수학자 Edouard Lucas에 의해 이루어졌다. 그는 1877년에 발표한 "Théorie des fonctions numériques simplement périodiques"라는 논문에서, Fibonacci 수열과 이와 관련된 행렬을 소개했다.
그리고 이 행렬이 피보나치 수열의 특징을 이용하여 피보나치 수열을 효율적으로 계산할 수 있다는 것이 알려지면서, 컴퓨터 과학 분야에서 널리 사용되고 있다.
다시 본론으로,

처음에 제시한 행렬을 확장하면 위의 행렬로 나타낼 수 있다. 이때, 왼쪽 부분을 r(n+1), 오른쪽 부분을 r(n)이라고 하면
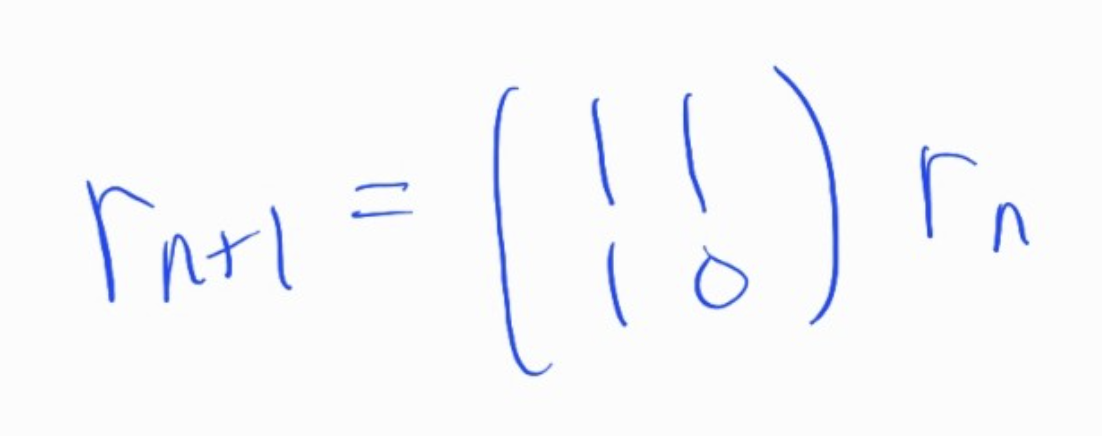
해당 식으로 표현할 수 있게 된다. 이는 n항에 'Fibonacci matrix'를 곱하면 n+1항이 된다는 의미이다.
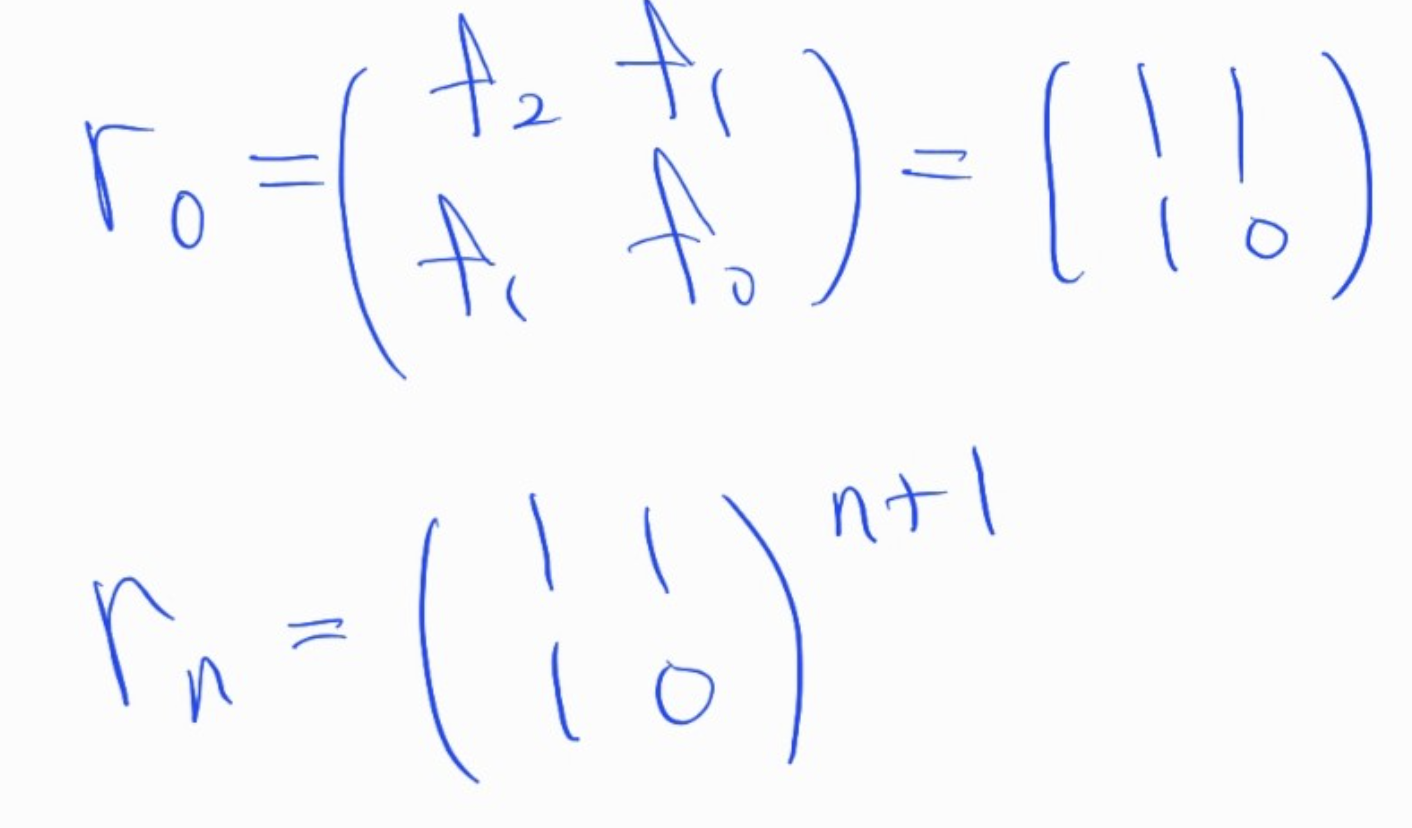
따라서 위와 같이 정리가 가능하다.
분할 정복
하지만 입력값이 10^18이기 때문에 10^18번을 곱하게 되면 n의 복잡도로 인해 시간초과가 발생한다.
따라서 '분할 정복' 방법이 필요하다.
분할 정복의 아이디어는 간단하다. 예를 들어, 2^10을 구할 때는 4번의 연산을 한다.
2^10 = 2^5 * 2^5
2^5 = 2^4 * 2^1
2^4 = 2^2 * 2^2
2^2 = 2^1 * 2^1
해당 문제를 예로 들어보자.
n=1000 일 때는,
1000 / 2 = 500 --> (Fibonacci matrix)^2
500 / 2 = 250 --> (Fibonacci matrix)^4
250 / 2 = 125 --> (Fibonacci matrix)^8
125는 홀수 --> (Fibonacci matrix)^8 * (Fibonacci matrix)^1
...
최종 코드
#include <iostream>
#include <vector>
#define MOD 1000000007
using namespace::std;
typedef vector<vector<long long>> mat;
mat operator*(mat &a, mat &b){
mat tmp(2, vector<long long>(2));
for(int i=0; i<2; i++){
for(int j=0; j<2; j++){
for(int k=0; k<2; k++){
tmp[i][j] += a[i][k] * b[k][j];
}
tmp[i][j] %= MOD;
}
}
return tmp;
}
int main(){
long long n;
scanf("%lld", &n);
mat r = {{1,0}, {0,1}};
mat a = {{1,1}, {1,0}};
while(n>0){
if(n%2 == 1){
r = r * a;
}
a = a * a;
n /= 2;
}
printf("%lld\n", r[1][0]);
}
'PS' 카테고리의 다른 글
| [C++] 백준 1261 - 알고스팟 (메모리 초과 이슈) (0) | 2023.03.15 |
|---|---|
| [C++] 백준 2407 - 조합 (0) | 2023.03.14 |
| [C++] 백준 1034 - 거짓말 (유니온 파인드는 모르겠고) (0) | 2023.03.03 |
| [C++] 백준 2638 - 치즈 (직관적인 접근) (1) | 2023.03.03 |
| [C++] 백준 1918 - 후위 표기식, 반례 (0) | 2023.03.03 |




댓글